网络正则化

Normalization

Batch Normalization

BN的公式：

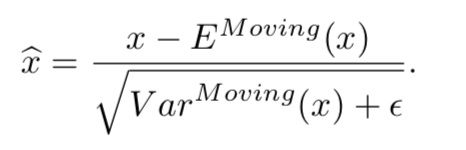
BN就是在深度神经网络训练时通过对每一个batch的数据采用均值和方差进行归一化，使得每一层神经网络的输入保持相同的分布，这样能够加快训练的速度。此外，因为在训练时，为每一次迭代求全局的均值和方差是不现实的，因此借鉴moment的方式对均值和方差进行更新，使得每一层归一化的均值和方差都不一样，也相当于引入了噪声，能够增加模型的鲁棒性，有效减少过拟合。

Layer Normalization

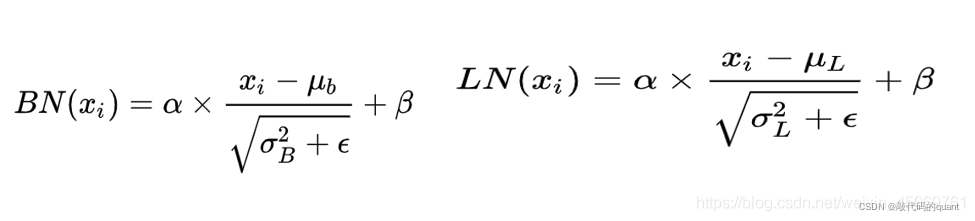
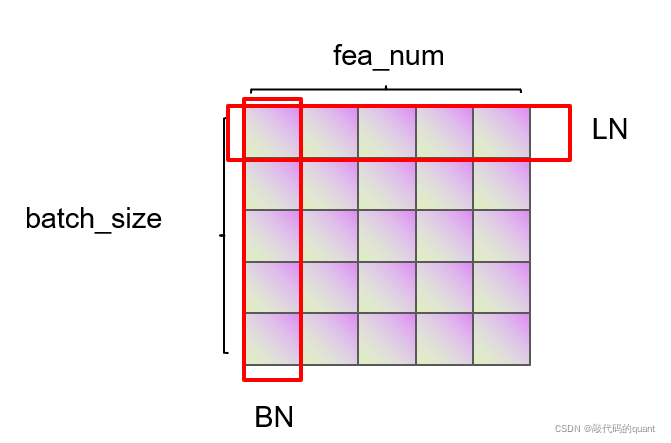
BN抹平了不同特征之间的大小关系，而保留了不同样本之间的大小关系。

不同图片的的同一通道的相对关系是保留的，即不同图片的同一通达的特征是可以比较的
同一图片的不同通道的特征则是失去了可比性

LN抹平了不同样本之间的大小关系，而保留了不同特征之间的大小关系。

同一句子中词义向量的相对大小是保留的，或者也可以说LayerNorm不改变词义向量的方向，只改变它的模。
不同句子的词义向量则是失去了可比性。

Batch Normalization 注意事项

BatchNorm避坑指南

论文链接

注意此语境下主要讨论的都是图像处理领域中的BatchNormalization应用问题，所以讨论的是BatchNorm2D。在训练阶段对形状为[N,C,H,W]的mini-batchX，BatchNorm首先计算各个通道上的均值和方差：

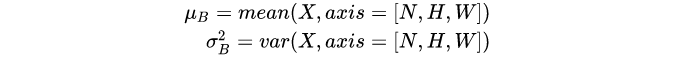
然后，在对特征x进行归一化：

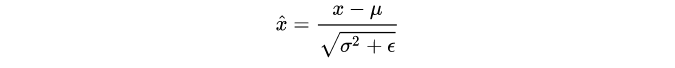
可以看到计算均值和方差是依赖batch的，这也就是BatchNorm的名字由来。在测试阶段，BatchNorm采用的均值和方差是从训练过程估计的全局统计量（population statistics）：$\mu_{pop}$和$\sigma_{pop}^2$，这两个参数也是从训练数据学习到的参数（但不是可训练参数，没有BP过程）。常规的做法在训练阶段采用EMA（ exponential moving average，指数移动平均，在TensorFlow中EMA产生的均值和方差称为moving_mean和moving_var，而PyTorch则称为running_mean和running_var）来估计：

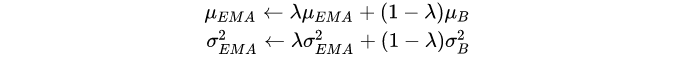
训练阶段采用的是mini-batch统计量，而测试阶段是采用全局统计量，这就造成了BatchNorm的训练和测试不一致问题，这个后面会详细讨论。

除了归一化，BatchNorm还包含对各个channel的特征做affine transform（增加特征表征能力）：

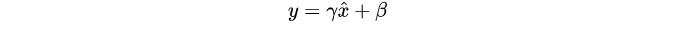
这里的$\gamma$和$\beta$是可训练的参数，但是这个过程其实没有batch的参与，从实现上等价于额外增加一个depthwise 1 × 1卷积层。BatchNorm的麻烦主要来自于mini-batch统计量的计算和归一化中，这个affine transform不是影响因素，所以后面的讨论主要集中在前面。

围绕着batch所能带来的问题，论文共讨论了BatchNorm的四个方面：

Population Statistics：EMA是否能够准确估计全局统计量以及PreciseBN；
Batch in Training and Testing：训练采用mini-batch统计量，而测试采用全局统计量，由此带来的不一致问题；
Batch from Different Domains：BatchNorm在multiple domains中遇到的问题；
Information Leakage within a Batch：BatchNorm所导致的信息泄露问题；

第二个应该是大家都熟知的问题，但是其实BatchNorm可能影响的方面是很多的，如域适应（domain adaptation)和对比学习中信息泄露问题。另外，这里讨论的4个方面也不是独立的，它们往往交织在一起。

Population Statistics

训练过程中的均值和方差是mini-batch计算出来的，但是在推理阶段往往是每次只处理一个sample，没有办法再计算依赖batch的统计量。BatchNorm采用的方法是训练过程中用EMA估计全局统计量，但是这个估计可能会够好：当$\lambda$较大时，每个iteration中mini-batch的统计量对全局统计量贡献很少，这会导致更新过慢；当$\lambda$较大时，每个iteration中mini-batch的统计量会起主导作用，导致估计值不能代表全局。一般情况$\lambda$取一个较大的值，如0.9或0.99，这是一个超参数。论文中在ResNet50的训练过程（256 GPU，每个GPU batch_size=32）随机选择模型的某个BatchNorm层的某个channel，绘制了其EMA mean以及population mean，这里的population mean采用当前模型在100 mini-batches的batch mean的平均值来估计，这个可以代表当前模型的全局统计量，对比图如下所示。在训练前期，从图a可以看到EMA mean和当前的batch mean是有距离的，而图b说明EMA mean是落后于当前模型的近似全局统计量的，但是到训练中后期EMA mean就比较准确了。

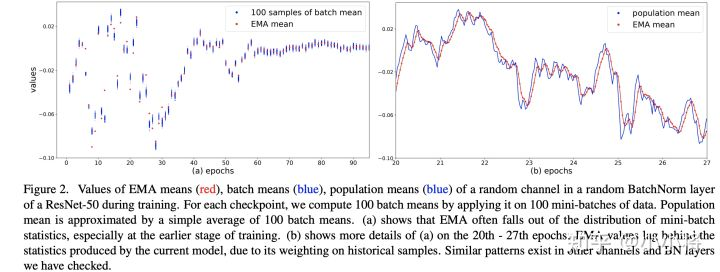
这说明EMA统计量在训练早期是有偏差的。一个准确的全局统计量应该是：使用整个训练集作为一个batch计算特征的均值和方差，但是这个计算成本太高了，论文中提出采用一种近似方法来计算：首先采用固定模型（训练好的）计算很多mini-batch；然后聚合每个mini-batch的统计量来得到全局统计量。假定共需要计算$N$个samples，batch_size为$B$，那么共计算$k=N/B$个mini-batch，记它们的统计量为$\mu_{B_i}$，$\sigma^2_{B_i}(i=1,…,k)$，那么全局统计量可以近似这样计算：

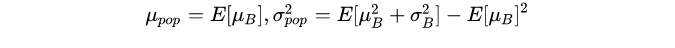
这其实只是一种聚合方式，论文附录也讨论了其它计算方式，结果是类似的。这种BatchNorm称为PreciseBN，具体代码实现可以参考fvcore.nn.precise_bn：

class _PopulationVarianceEstimator:
    """
    Alternatively, one can estimate population variance by the sample variance
    of all batches combined. This needs to use the batch size of each batch
    in this function to undo the bessel-correction.
    This produces better estimation when each batch is small.
    See Appendix of the paper "Rethinking Batch in BatchNorm" for details.
    In this implementation, we also take into account varying batch sizes.
    A batch of N1 samples with a mean of M1 and a batch of N2 samples with a
    mean of M2 will produce a population mean of (N1M1+N2M2)/(N1+N2) instead
    of (M1+M2)/2.
    """

    def __init__(self, mean_buffer: torch.Tensor, var_buffer: torch.Tensor) -> None:
        self.pop_mean: torch.Tensor = torch.zeros_like(mean_buffer) # population mean
        self.pop_square_mean: torch.Tensor = torch.zeros_like(var_buffer) # population variance 
        self.tot = 0 # total samples
    
    # update per mini-batch, is called by `update_bn_stats`
    def update(
        self, batch_mean: torch.Tensor, batch_var: torch.Tensor, batch_size: int
    ) -> None:
        self.tot += batch_size
        batch_square_mean = batch_mean.square() + batch_var * (
            (batch_size - 1) / batch_size
        )
        self.pop_mean += (batch_mean - self.pop_mean) * (batch_size / self.tot)
        self.pop_square_mean += (batch_square_mean - self.pop_square_mean) * (
            batch_size / self.tot
        )

    @property
    def pop_var(self) -> torch.Tensor:
        return self.pop_square_mean - self.pop_mean.square()

论文中以ResNet50的训练为例对比了EMA和PreciseBN的效果，如下图所示，可以看到PreciseBN比EMA效果更加稳定，特别是训练早期（此时模型未收敛），虽然最终两者的效果接近。

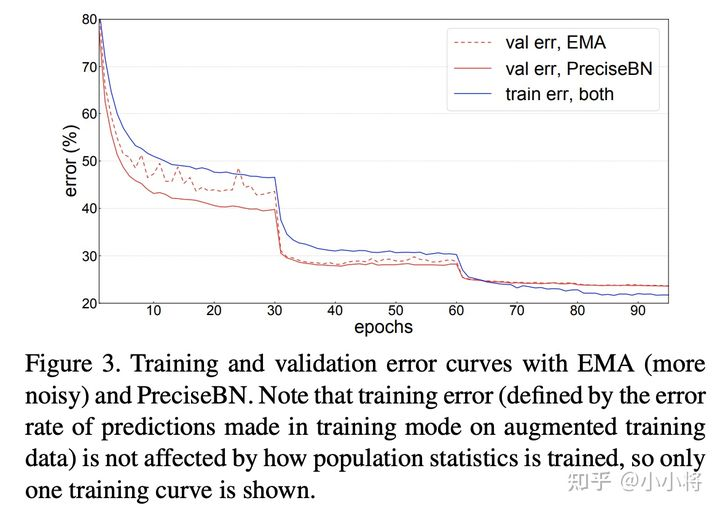
进一步地，如果训练采用更大的batch size，实验发现EMA在训练过程中的抖动更大，但此时PreciseBN效果比较稳定。当采用larger batch训练时，学习速率增大，而且EMA更新次数减少，这些都会对EMA产生较大影响。综上，虽然EMA和PreciseBN最终效果接近（因此EMA的缺点往往被忽视），但是在模型未收敛的训练早期，PreciseBN更加稳定，像强化学习需要在训练早期评估模型效果这种场景，PreciseBN能带来更加稳定可靠的结果。

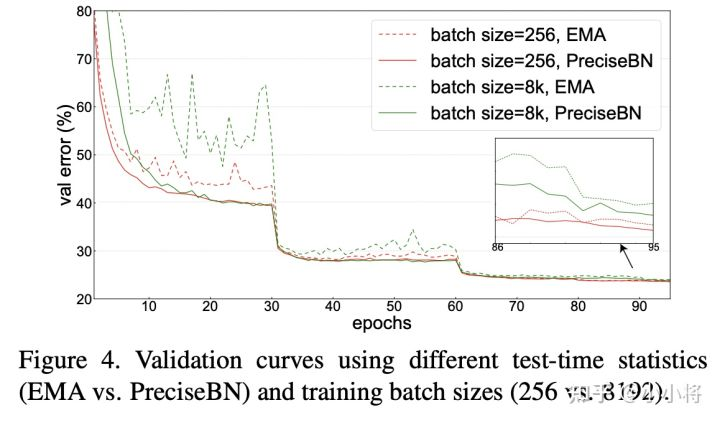
此外，论文也通过实验证明了PreciseBN只需要$10^3-10^4$ samples就可以得到比较好的结果，以ImageNet训练为例，采用PreciseBN评估只需要增加0.5%的训练时间。

另外，论文里还对比了batch size对PreciseBN的影响。这里先理清楚两个概念：（1）normalization batch size（NBS）：实际计算统计量的mini-batch的size；（2）total batch size或者SGD batch size：每个iteration中mini-batch的size，或者说每执行一次SGD算法的batch size；两者在多卡训练过程是不等同的（此时NBS是per-GPU batch size，而SyncBN可以实现两者一致）。从结果来看，NBS较小时，模型效果会变差，但是PreciseBN的batch size是相对NBS独立的，所以选择batch size 时PreciseBN可以取得稳定的效果，并且在NBS较小时相比EMA提升效果。

Batch in Training and Testing

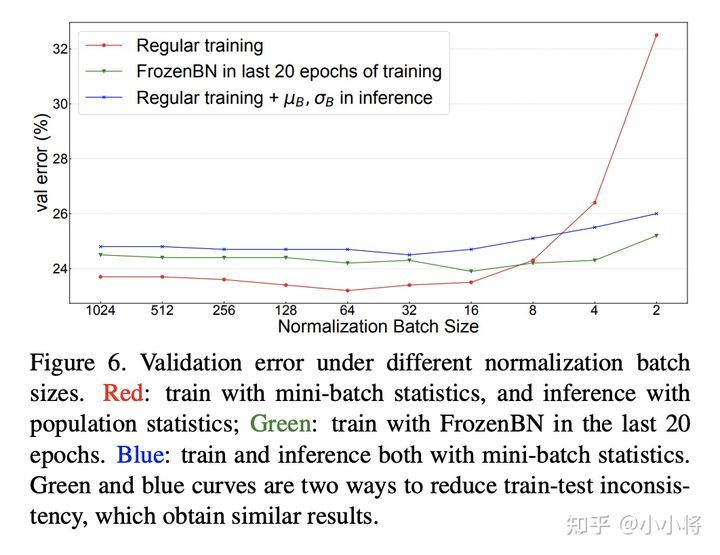
前面已经说过BatchNorm在训练时采用的是mini-batch统计量，而测试时采用的全局统计量，这就导致了训练和测试的不一致性，从而带来对模型性能的影响。为此，论文还是以ResNet50训练为例分析这种不一致带来的影响，这里还同时比较了不同NBS带来的差异（SGD batch size固定在1024，此时NBS从2~1024变化），分别对比不同NBS下的三个指标：（1）采用mini-batch统计量在训练集上的分类误差；（2）采用mini-batch统计量在验证集上的分类误差；（3）采用全局统计量在验证集上的分类误差。这里（1）和（3）其实是常规评估方法，而（2）往往不会这样做，但是（1）和（2）就保持一致了（训练和测试均采用mini-batch统计量）。对比结果如下所示，从中可以得到三个方面的结论：

training noise：训练集误差随着NBS增大而减少，这主要是由于SGD训练噪音所导致的，当NBS较小时，mini-batch统计量波动大导致优化困难，从而产生较大的训练误差；
generalization gap：对比（1）和（2），两者均采用mini-batch统计量，差异就来自数据集不同，这部分性能差异就是泛化gap；
train-test inconsistency：对比（2）和（3），两者数据集一样，但是（2）采用mini-batch统计量，而（3）采用全局统计量，这部分性能差异就是训练和测试不一致所导致的；

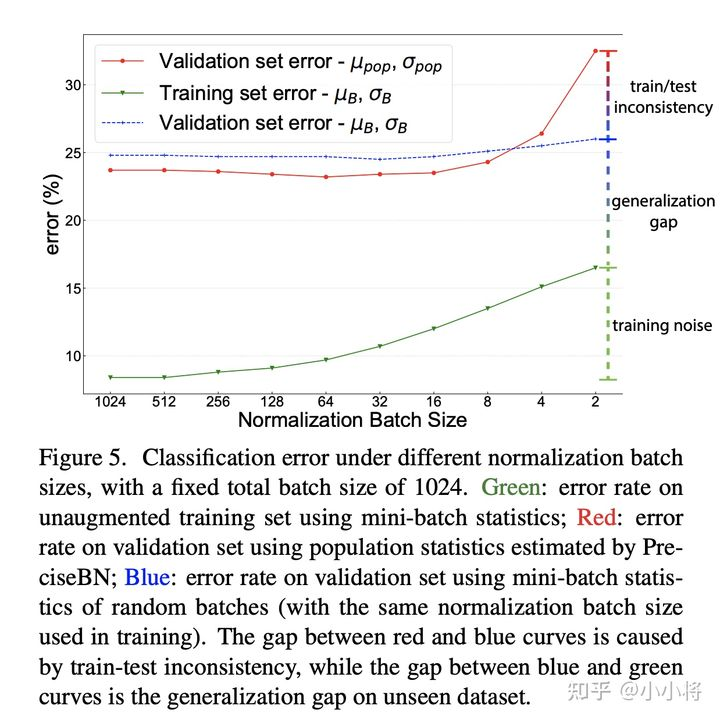
另外，我们可以看到当NBS较小时，（2）和（3）的性能差距是比较大的，这说明如果训练的NBS比较小时在测试时采用mini-batch统计量效果会更好，此时保持一致是比较重要的（这点至关重要）。当NBS较大时，（2）和（3）的差异就比较小，此时mini-batch统计量越来越接近全局统计量。

虽然NBS较小时，在测试时采用mini-batch统计量效果更好，但是在实际场景中几乎不会这样处理（一般情况下都是每次处理一个样本）。不过还是有一些特例，比如两阶段检测模型R-CNN中，R-CNN的head输入是每个图像的一系列region-of-interest (RoIs)，一般情况下一个图像会有$10^2-10^3$个RoIs，实际情况这些RoIs是组成batch进行处理的，训练过程是所有图像的RoIs，而测试时是单个图像的RoIs组成batch，在这种情况中测试时就可以选择mini-batch统计量。这里以Mask R-CNN为实验模型，将默认的2fc box head

（2个全连接层）换成4conv1fc head（4个卷积层加一个，并且在box head和mask head的每个卷积层后面都加上BatchNorm层，实验结果如下，可以看到采用mini-batch统计量是优于采用全局统计量的，另外在训练过程中每个GPU只用一张图像时，此时测试时采用全局统计量效果会很差，这里有另外的过拟合问题存在，后面再述（BatchNorm导致的信息泄露）。另外R-CNN的head还存在另外的一种训练和测试的inconsistency：训练时mini-batch是正负样本抽样的，而测试时是按score选取的topK，mini-batch的分布就发生了变化。

另外一个避免训练和测试的inconsistency可选方案是训练也采用全局统计量，常用的方案是Frozen BatchNorm (FrozenBN)（训练中直接采用EMA统计量模型无法训练），FrozenBN指的是采用一个提前算好的固定全局统计量，此时BatchNorm的训练优化就只有一个linear transform了。FrozenBN采用的情景是将一个已经训练好的模型迁移到其它任务，如在ImageNet训练的ResNet模型在迁移到下游检测任务时一般采用FrozenBN。不过我们也可以在模型的训练过程中采用FrozenBN，论文中还是以ResNet50为例，在前80个epoch采用正常的BN训练，在后20个epoch采用FrozenBN，对比效果如下，可以看到FrozenBN在NBS较小时也是表现较好，优于测试时采用mini-batch统计量，这不失为一种好的方案。这里值得注意的是当NBS较大时，FrozenBN还是测试时采用mini-batch统计量均差于常规方案（BN训练，测试时采用全局统计量）。

包含BatchNorm的模型训练过程包含两个学习过程：一是模型主体参数是通过SGD学习得到的（SGD training），二是全局统计量是通过EMA或者PreciseBN从训练数据中学习得到（population statistics training）。当训练数据和测试数据分布不同时，我们称之为domain shift，这个时候学习得到的全局统计量就可能会在测试时失效，这个问题已经有论文提出要采用Adaptive BatchNorm来解决，即在测试数据上重新计算全局统计量。这里还是以ResNet50为例（SGD batch size为1024，NBS为32），用ImageNet-C数据集（ImageNet的扰动版本，共三种类型：contrast，gaussian noise和jpeg compression）来评估domain shift问题，结果如下：

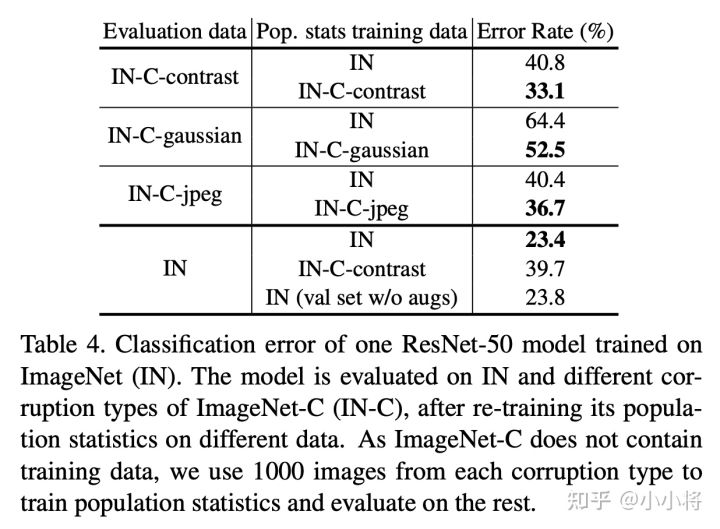
从表中可以明显看出：当出现domain shift问题后，采用Adaptive BatchNorm在target domain数据集上重新计算全局统计量可以提升模型效果。不过从表最后一行可以看到，如果在ImageNet验证集上重新计算统计量（直接采用inference-time预处理），最终效果要稍微差于原来结果（23.4 VS 23.8），这可能说明如果不存在明显的domain shift，原始处理方式是最好的。

除了domain shift，训练数据存在multi-domain也会对BatchNorm产生影响，这个问题更复杂了。这里以RetinaNet模型来说明multi-domain的出现可能出现的问题。RetinaNet的head包含4个卷积层以及最终的分类器和回归器，其输入是来自不同尺度的5个特征（$P_3, P_4, P_5,P_6,P_7$)，这可以看成5个不同的domain。head在5个特征上是共享的，默认head是不包含BatchNorm，当我们在head的每个卷积后加上BatchNorm后，问题就变得复杂了。首先，首先就是SGD训练过程mini-batch统计量的计算，明显有两种不同处理方式，一是对不同domain的特征输入单独计算mini-batch统计量并单独归一化，二是将所有domain的特征concat在一起，计算一个mini-batch统计量来归一化。这两种处理方式如下所示：

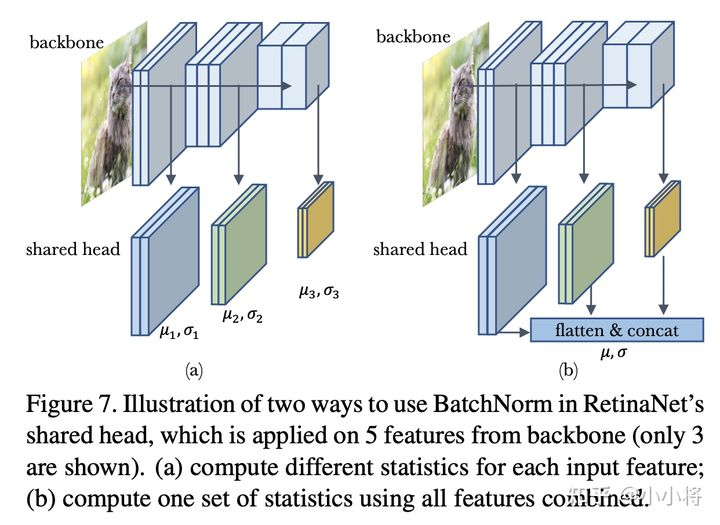
这里记上述SGD训练过程中的两种方式分别为domain-specific statistics和shared statistics。对于学习全局统计量，同样存在对应的两种方式，即每个domain的特征单独学习一套全局统计量，还是共享一套全局统计量。对于BatchNorm的affine transform layer也存在两种选择：每个domain一套参数还是共享参数。不同组合的模型效果如下表所示：

从表中结果可以总结两个结论：（1）SGD training和population statistics training保持一致非常重要，此时都可以取得较好的结果（行1，行4和行6）；（2）affine transform layer无论单独参数还是共享基本不影响结果。这里的一个小插曲是如果直接在head中加上BatchNorm，其实对应的是行3，其实这是因为不同尺度的特征是序列处理的，这就造成了SGD training其实是domain-specific的，但全局统计量是共享的，此时效果就较差，所以大部分实现中要不然不用norm，要不然就用GroupNorm。不同组合的实现代码如下：

# 简单地加上BN，注意forward时，不同特征是串行处理的，那么SGD training其实是domain-specific的，
# 但是只维持一套全局统计量，所以测试时又是共享的
class RetinaNetHead_Row3:
    def __init__(self, num_conv, channel):
        head = []
        for _ in range(num_conv):
            head.append(nn.Conv2d(channel, channel, 3))
            head.append(nn.BatchNorm2d(channel))
        self.head = nn.Sequential(∗head)
    def forward(self, inputs: List[Tensor]):
        return [self.head(i) for i in inputs]

# 如果要共享，那么在forward时对特征进行concat来统一计算并归一化 
class RetinaNetHead_Row1(RetinaNetHead_Row3):
    def forward(self, inputs: List[Tensor]):
        for mod in self.head:
            if isinstance(mod, nn.BatchNorm2d):
                # for BN layer, normalize all inputs together
                shapes = [i.shape for i in inputs]
                spatial_sizes = [s[2] ∗ s[3] for s in shapes]
                x = [i.flatten(2) for i in inputs]
                x = torch.cat(x, dim=2).unsqueeze(3)
                x = mod(x).split(spatial_sizes, dim=2)
                inputs = [i.view(s) for s, i in zip(shapes, x)]
            else:
                # for conv layer, apply it separately
                inputs = [mod(i) for i in inputs]
        return inputs

# 另外一种简单的处理方式是每个特征采用各自的BN
class RetinaNetHead_Row6:
    def __init__(self, num_conv, channel, num_features):
        # num_features: number of features coming from
        # different FPN levels, e.g. 5
        heads = [[] for _ in range(num_levels)]
        for _ in range(num_conv):
            conv = nn.Conv2d(channel, channel, 3)
            for h in heads:
                # add a shared conv and a domain−specific BN
                h.extend([conv, nn.BatchNorm2d(channel)])
        self.heads = [nn.Sequential(∗h) for h in heads]
    def forward(self, inputs: List[Tensor]):
        # end up with one head for each input
        return [head(i) for head, i in
            zip(self.heads, inputs)]

对于行2和行4，可以通过训练好的行1和行3模型重新在训练数据上计算domain-specific全局统计量即可，在实现时，可以如下：

class CycleBatchNormList(nn.ModuleList):
    """
    A hacky way to implement domain-specific BatchNorm
    if it's guaranteed that a fixed number of domains will be
    called with fixed order.
    """

    def __init__(self, length, channels):
        super().__init__([nn.BatchNorm2d(channels, affine=False) for k in range(length)])
        # shared affine, domain-specific BN
        self.weight = nn.Parameter(torch.ones(channels))
        self.bias = nn.Parameter(torch.zeros(channels))
        self._pos = 0

    def forward(self, x):
        ret = self[self._pos](x)
        self._pos = (self._pos + 1) % len(self)

        w = self.weight.reshape(1, -1, 1, 1)
        b = self.bias.reshape(1, -1, 1, 1)
        return ret * w + b

# 训练好模型，我们可以重新将BN层换成以上实现，就可以在训练数据上重新计算domain-specific全局统计量

RetinaNet面临的其实是特征层面的multi-domain问题，而且每个batch中的各个domain是均匀的。如果是数据层面的multi-domain，其面临的问题将会复杂，此时domain的分布比例也是多变的（BatchNorm可能会偏向训练数据较多的那个domain），但是总的原则是尽量减少不一致性，因为consistency is crucial。

Information Leakage within a Batch

BatchNorm面临的另外一个挑战，就是可能出现信息泄露，这里所说的信息泄露指的是模型学习到了利用mini-batch的信息来做预测，而这些其实并不是我们要学习的，因为这样模型可能难以对mini-batch里的每个sample单独做预测。

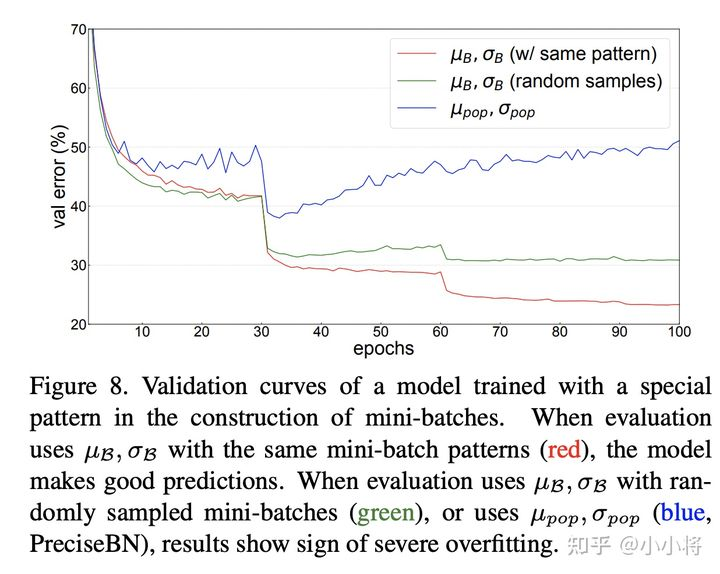
比如BatchNorm的作者曾做过这样一个实验，在ResNet50的训练过程中，NBS=32，但是保证里面包含16个类别，每个类别有2个图像，这样一种特殊的设计要模型在训练过程中强制记忆了这种模式（可能是每个mini-batch中必须有同类别存在），那么在测试时如果输入不是这种设计，效果就会变差。这个在验证集上不同处理结果如上所示，可以看到测试时无论是采用全局统计量还是random mini-batch统计量，效果均较差，但是如果采用和训练过程同样的模式，效果就比较好。这其实也从侧面说明保持一致是多么的重要。

前面说过，如果在R-CNN的head加入BatchNorm，那么在测试时采用mini-batch统计量会比全局统计量会效果更好，这里面其实也存在信息泄露的问题。对于每个GPU只有一个image的情况，每个mini-batch里面的RoIs全部来自于一个图像，这时候模型就可能依赖mini-batch来做预测，那么测试时采用全局统计量效果就会差了，对于每个GPU有多个图像时，情况还稍好一些，所以原来的结果中单卡单图像效果最差。一种解决方案是采用shuffle BN，就是head进行处理前，先随机打乱所有卡上的RoIs特征，每个卡分配随机的RoIs，这样就避免前面那个可能出现的信息泄露，head处理完后再shuffle回来，具体处理流程如下所示：

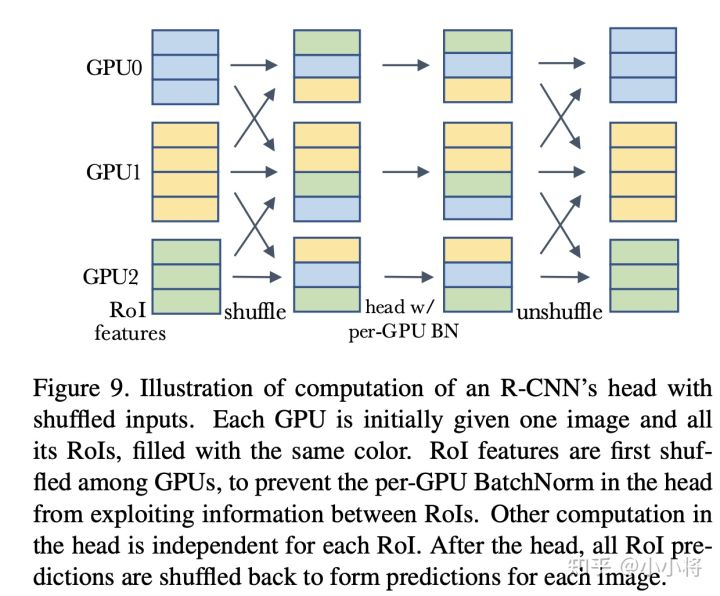
这个具体的代码实现见mask_rcnn_BNhead_shuffle.py。其实在MoCo中也使用了shuffle BN来防止信息泄露。另外还是可以采用SyncBN来避免这种问题（或者说是global BN，增大了mini-batch，这样就可以减弱上述影响）。具体的对比结果如下所示，可以看到采用shuffle BN和SyncBN均可以避免信息泄露，得到较好的效果。注意shuffle BN的 cross-GPU synchronization要比SyncBN要少，效率更高一些。

另外一个常见的场景是对比学习中信息泄露，因为对比学习往往需要对同一个图像做不同的augmentations来作为正样本，这其实一个sample既当输入又当目标，mini-batch可能会泄露信息导致模型学习不到好的特征（普通的BN是per-GPU normalize，这意味正样本的计算都在同一个local mini-batch中）。MoCo采用的是shuffle BN（其实是encode_k采用shuffle BN，这样两次正样本的计算就有区别），而SimCLR和BYOL采用的是SyncBN（扩大mini-batch减少影响）。另外旷视提出的Momentum^2 Teacher来采用moving average statistics来防止信息泄露。一个插曲是这篇博客指出其实BN才是不需要负样本的BYOL成功的关键，因为BN隐式地引入了负样本从而形成了对比学习，虽然后面BYOL又证明不需要BN也可以取得好的效果，但是还是比BN差一点。这说明BN确实能够隐式编码batch信息。

总结

一个简单的BatchNorm，如果我们使用不当，往往会出现一些让人意料的结果，所以要谨慎处理。总结来看，主要有如下结论和指南：

模型在未收敛时使用EMA统计量来评估模型是不稳定的，一种替代方案是PreciseBN；
BatchNorm本身存在训练和测试的不一致性，特别是NBS较少时，这种不一致会更强，可用的方案是测试时也采用mini-batch统计量或者采用FrozenBN；
在domain shift场景中，最好基于target domain数据重新计算全局统计量，在multi-domain数据训练时，要特别注意处理的一致性；
BatchNorm会存在信息泄露的风险，这处理mini-batch时要防止特殊的出现。

我个人认为下列两个原则可能是普适的：

尽量减少训练和测试的不一致行为，不一致行为会导致测试时性能恶化；
尽量减少训练过程的bias而应适当增加noise，以防止模型训练走捷径而学习到无法泛化的特征。

Dropout

dropout在训练时，以一定的概率p来drop掉相应的神经网络节点，以(1-p)的概率来retain相应的神经网络节点，这相当于每一次训练时模型的网络结构都不一样，也可以理解为训练时添加了噪声，所以能够有效减少过拟合。
问题呢，是出在测试时，因为训练的时候以概率p drop了一些节点，比如dropout设置为0.5，隐藏层共有6个节点，那训练的时候有3个节点的值被丢弃，而测试的时候这6个节点都被保留下来，这就导致了训练和测试的时候以该层节点为输入的下一层的神经网络节点获取的期望会有量级上的差异。为了解决这个问题，在训练时对当前dropout层的输出数据除以（1-p），之后再输入到下一层的神经元节点，以作为失活神经元的补偿，以使得在训练时和测试时每一层的输入有大致相同的期望。

Normalization和Dropout搭配

产生的问题：方差偏移

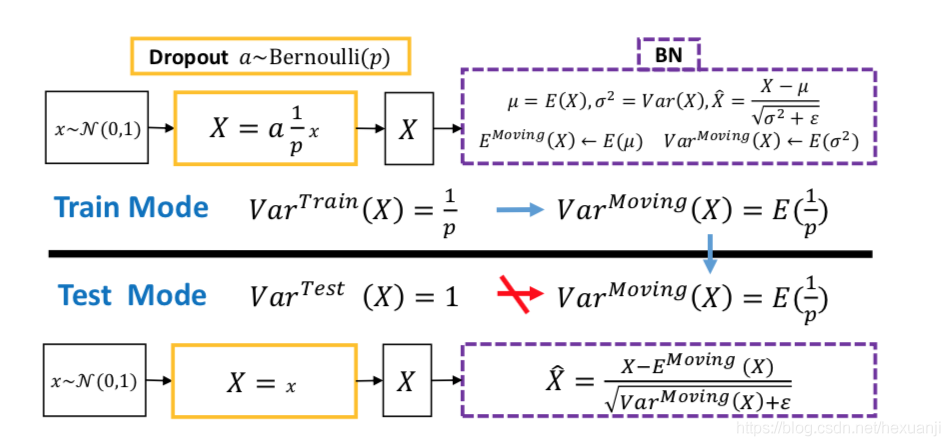
首先，先明确dropout和BN结合使用使模型性能下降的连接方式，用通俗的话讲，就是你先在网络的内部使用dropout，随后再跟上一个BN层，而且这个BN层还不止一个。那么问题出在哪呢？原因有二。首先，如上图所示，因为训练时采用了dropout，虽然通过除以(1-p)的方式来使得训练和测试时，每个神经元输入的期望大致相同，但是他们的方差却不一样。第二，BN是采用训练时得到的均值和方差对数据进行归一化的，现在dropout层的方差都不一样了，一步错步步错，最终导致输出不准确，影响最后的性能。

针对方差偏移，论文给出了两种解决方案：

拒绝方差偏移，只在所有BN层的后面采用dropout层，现在大部分开源的模型，都在网络的中间加了BN，你也就只能在softmax的前一层加加dropout了，我亲自试过，效果还行，至少不会比不加dropout差。还有另外一种方法是模型训练完后，固定参数，以测试模式对训练数据求BN的均值和方差，再对测试数据进行归一化，论文证明这种方法优于baseline。
dropout原文提出了一种高斯dropout，论文再进一步对高斯dropout进行扩展，提出了一个均匀分布Dropout，这样做带来了一个好处就是这个形式的Dropout（又称为“Uout”）对方差的偏移的敏感度降低了，总得来说就是整体方差偏地没有那么厉害了。可以看得出来实验性能整体上比第一个方案好，这个方法显得更加稳定。