模型优化 kaiming初始化的推导
权重初始化 为什么需要权重初始化 网络训练的过程中,容易出现梯度消失(梯度特别的接近0)和梯度爆炸(梯度特别的大)的情况,导致大部分反向传播得到的梯度不起作用或者起反作用。研究人员希望能够有一种好的权重初始化方法:让网络前向传播或者反向传播的时候,卷积的输出和前传的梯度比较稳定。合理的方差既保证了数值一定的不同,又保证了数值一定的稳定。(通过卷积权重的合理初始化, 让计算过程中的数值分布稳定)
推导的先验知识
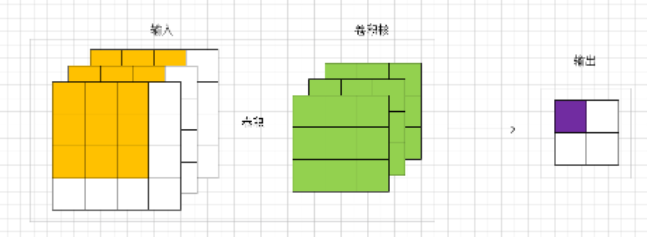
参照上面的卷积图,对输入的特征图进行的卷积。具体要研究的是输出的一个点的方差(紫色点)。所以是通过黄色的输入(个)和绿色的卷积参数(个)去计算一个输出值(紫色输出)的方差。 一个点 对应于原论文里面的说法为a response。 感觉这个是理解权重初始化的重点。基于独立同分布的强假设:输入的每个值都是独立同分布的,所以和独立同分布的参数进行卷积得到结果的分布也是相同的。所以其他的3个输出点的方差也是一样的。进一步说,虽然输入是个不同的值。但是我们可以这样认为:有一个满足某分布的随机变量,然后随机抽样48次,这48个值就可以组成了输入,且独立同分布(也可称输入的每个像素点是独立同分布的)。 卷积的参数也可以这么认为。那么我们可以用一个随机变量表示48个输入,也可以用一个随机变量表示27个卷积参数,亦可以用一个随机变量表示4个输出值。
公式 $$
上式表示独立随机变量之和的方差等于各变量的方差之和,如果$X_1$和$X_2$还是同分布的,那么$var(X_1)=var(X_2)->var(X_1)+var(X_2)=2var(X_1)=2var(X_2)$。将这个应用在卷积求和的那一步(卷积先乘,再求和)。
$$
上式是通过期望求方差的公式,方差等于平方的期望减去期望的平方。如果$E(X)=0$,那么$var(X)=E(X^2)$。
$$
上式式独立变量乘积的一个公式(协方差为0)如果$E(X)=E(Y)=0$,那么$var(XY)=var(X)var(Y)$。
kaiming初始化
前向传播的时候, 每一层的卷积计算结果的方差为1.
反向传播的时候, 每一 层的继续往前传的梯度方差为1(因为每层会有两个梯度的计算,一个用来更新当前层的权重,一个继续传播,用于前面层的梯度的计算。)
源码 方差的计算需要两个值:gain 和fan。gain 值由激活函数决定。fan 值由权重参数的数量和传播的方向决定。fan_in 表示前向传播,fan_out 表示反向传播。
1 2 3 4 5 6 7 8 def kaiming_normal_ (tensor, a=0 , mode='fan_in' , nonlinearity='leaky_relu' ): fan = _calculate_correct_fan(tensor, mode) gain = calculate_gain(nonlinearity, a) std = gain / math.sqrt(fan) with torch.no_grad(): return tensor.normal_(0 , std)
下面的代码根据网络设计时卷积权重的形状 和前向传播还是反向传播,进行fan 值的计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def _calculate_fan_in_and_fan_out (tensor ): dimensions = tensor.dim() if dimensions < 2 : raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions" ) if dimensions == 2 : fan_in = tensor.size(1 ) fan_out = tensor.size(0 ) else : num_input_fmaps = tensor.size(1 ) num_output_fmaps = tensor.size(0 ) receptive_field_size = 1 if tensor.dim() > 2 : receptive_field_size = tensor[0 ][0 ].numel() fan_in = num_input_fmaps * receptive_field_size fan_out = num_output_fmaps * receptive_field_size return fan_in, fan_out def _calculate_correct_fan (tensor, mode ): mode = mode.lower() valid_modes = ['fan_in' , 'fan_out' ] if mode not in valid_modes: raise ValueError("Mode {} not supported, please use one of {}" .format (mode, valid_modes)) fan_in, fan_out = _calculate_fan_in_and_fan_out(tensor) return fan_in if mode == 'fan_in' else fan_out
下面是通过不同的激活函数返回一个gain 值,当然也说明了是recommend。可以自己修改。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 def calculate_gain (nonlinearity, param=None ): r"""Return the recommended gain value for the given nonlinearity function. The values are as follows: ================= ==================================================== nonlinearity gain ================= ==================================================== Linear / Identity :math:`1` Conv{1,2,3}D :math:`1` Sigmoid :math:`1` Tanh :math:`\frac{5}{3}` ReLU :math:`\sqrt{2}` Leaky Relu :math:`\sqrt{\frac{2}{1 + \text{negative\_slope}^2}}` ================= ==================================================== Args: nonlinearity: the non-linear function (`nn.functional` name) param: optional parameter for the non-linear function Examples: >>> gain = nn.init.calculate_gain('leaky_relu', 0.2) # leaky_relu with negative_slope=0.2 """ linear_fns = ['linear' , 'conv1d' , 'conv2d' , 'conv3d' , 'conv_transpose1d' , 'conv_transpose2d' , 'conv_transpose3d' ] if nonlinearity in linear_fns or nonlinearity == 'sigmoid' : return 1 elif nonlinearity == 'tanh' : return 5.0 / 3 elif nonlinearity == 'relu' : return math.sqrt(2.0 ) elif nonlinearity == 'leaky_relu' : if param is None : negative_slope = 0.01 elif not isinstance (param, bool ) and isinstance (param, int ) or isinstance (param, float ): negative_slope = param else : raise ValueError("negative_slope {} not a valid number" .format (param)) return math.sqrt(2.0 / (1 + negative_slope ** 2 )) else : raise ValueError("Unsupported nonlinearity {}" .format (nonlinearity))
下面是kaiming初始化均匀分布的计算。为啥还有个均匀分布?权重初始化推导的只是一个方差, 并没有限定是正态分布 ,均匀分布也是有方差的,并且均值为0的时候,可以通过方差算出均匀分布的最小值和最大值。
1 2 3 4 5 6 7 8 def kaiming_uniform_ (tensor, a=0 , mode='fan_in' , nonlinearity='leaky_relu' ): fan = _calculate_correct_fan(tensor, mode) gain = calculate_gain(nonlinearity, a) std = gain / math.sqrt(fan) bound = math.sqrt(3.0 ) * std with torch.no_grad(): return tensor.uniform_(-bound, bound)
数学原理 kaiming初始化的推导过程只包含卷积和ReLU激活函数,默认是vgg类似的网络,没有残差,concat之类的结构, 也没有BN层。
$$
此处,Y_l表示某个位置的输出值,X_l表示被卷积的输入,有kxkx