本系列是参考冈萨雷斯《数字图像处理》与斯坦福CS131课程进行自我总结而成的数字图像处理基础知识。

概念

空间域：指的是图像平面本身。空间域中的图像处理方法直接对图像中的像素进行处理
变换域：如频率域。对图像进行变换，变换到变换域中。在变换域中进行处理，处理之后再对图像进行反变换，把结果带回空间域。

空间域变换表达式

$$ g(x,y) = T[ f(x,y) ] \tag{1}$$

式中$f(x,y)$是输入图像，$g(x,y)$是输出图像，$T$是在点$(x,y)$的一个领域上定义的针对$f$的算子，或者叫变换函数。

灰度变换

灰度变换作为增强图像的一种方法，通常用于调整图像对比度，使得图像满足于“特定”的要求。

常用灰度变换函数有

反转变换
对数变换
幂律变换
分段线性函数变换
比特平面分层 - 可用于图像压缩与重构

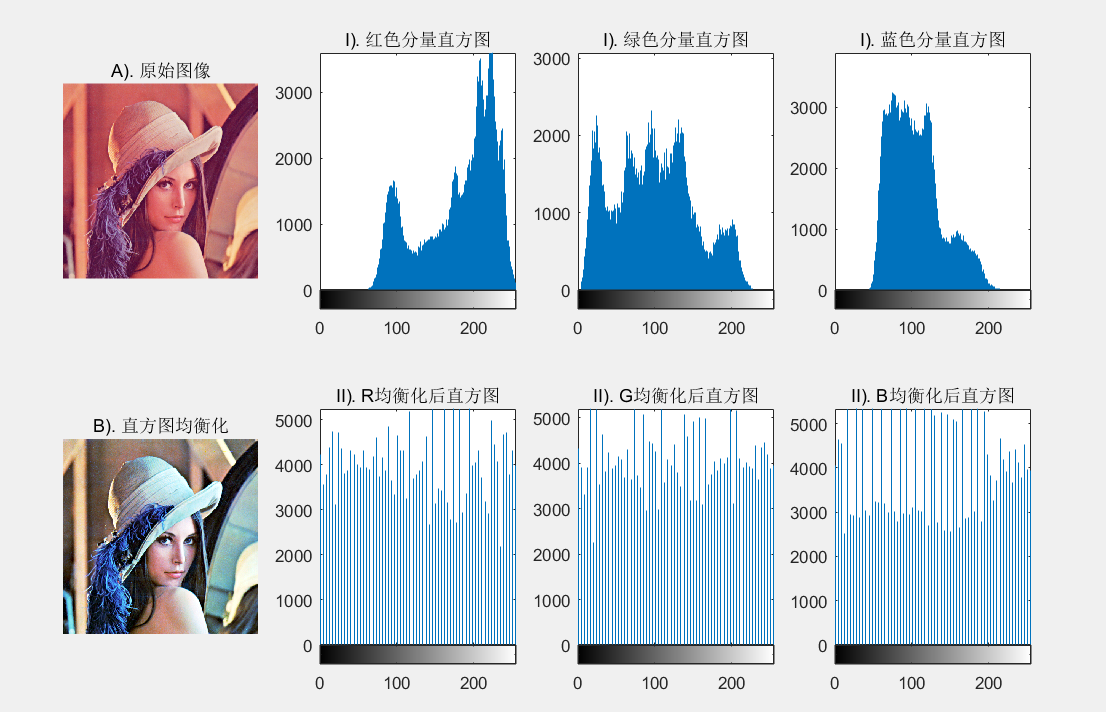
图像直方图

参考：https://blog.csdn.net/qq_38701868/article/details/89215881

简单来说，直方图就是对数据进行统计的一种方法，并且将统计值组织到一系列实现定义好的 bin 当中。其中， bin 为直方图中经常用到的一个概念，可以译为 “直条” 或 “组距”，其数值是从数据中计算出的特征统计量，这些数据可以是诸如梯度、方向、色彩或任何其他特征。且无论如何，直方图获得的是数据分布的统计图。通常直方图的维数要低于原始数据。

图像直方图（Image Histogram）是用以表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素数。这种直方图中，横坐标的左侧为纯黑、较暗的区域，而右侧为较亮、纯白的区域。因此一张较暗图片的直方图中的数据多集中于左侧和中间部分，而整体明亮、只有少量阴影的图像则相反。

图像直方图的数学定义如下
$$ h(r_k) = n_k , k=0,1,2, \cdots ,L-1 \tag{2}$$
更加常用的是归一化后的图像直方图
$$ p(r_k) = \frac{h(r_k)}{MN} = \frac{n_k}{MN} \tag{3} $$

图像直方图示意

空间滤波基础

线性滤波器

线性空间滤波器在图像$f$和滤波器核$w$之间执行乘积运算。核是一个阵列，其大小定义了运算的邻域，其系数决定了该滤波器的性质。

相关滤波器公式
$$ g(x,y) = \sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s,t)f(x+s,y+t) \tag{4}$$
该公式适用于任何奇数大小的核。

形象化表示如下图

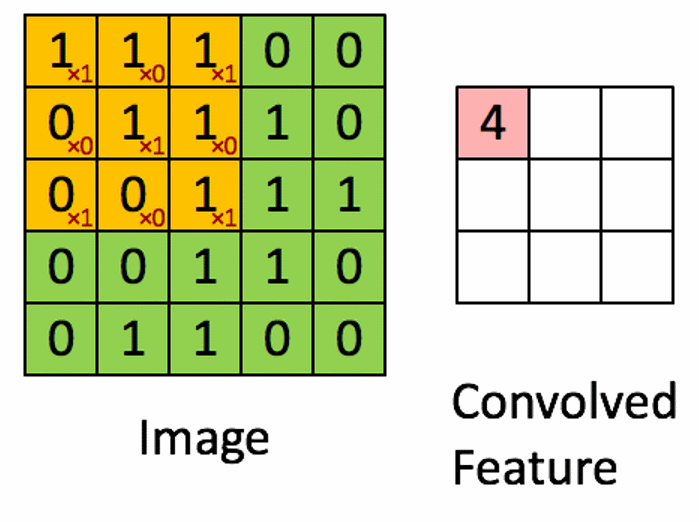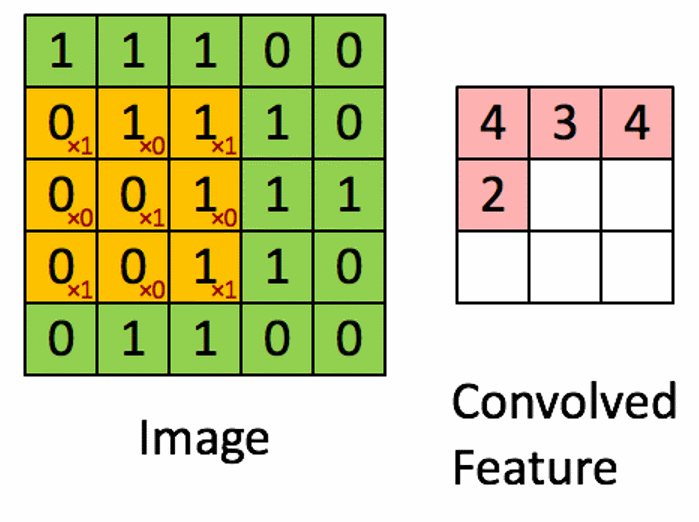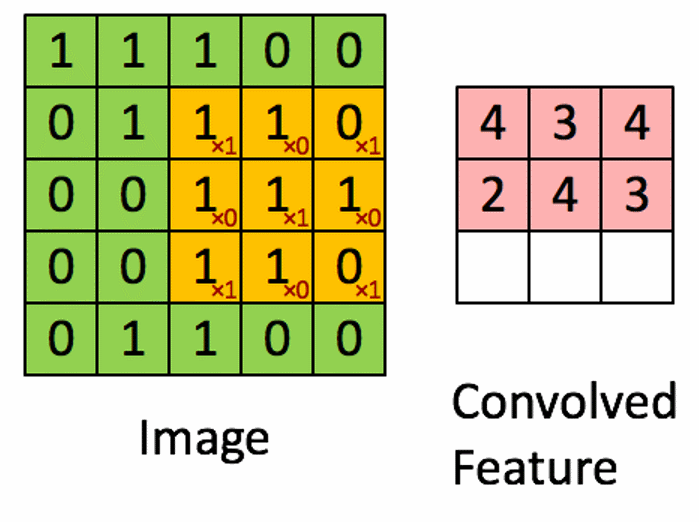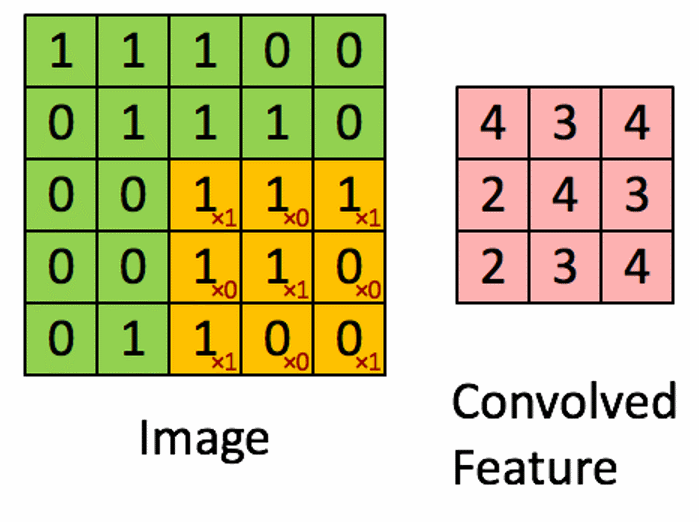
空间滤波示意图

图片参考：https://blog.csdn.net/IT_charge/article/details/105563188

注意到如果从图像的左上角作为第一个元素计算，有一部分的元素并没有定义，这是后通常采用填充的方法进行运算，一般填充0，但是并不只有填充0这一种方法。而上图采用的是缩小滤波范围的方法，即不从左上角第一元素开始。

卷积和相关的一些基本运算性质

破折号表示性质不成立

性质	卷积	相关
交换律	$fg=gf$	-
结合律	$f(gh)=(fg)h$	-
分配律	$f*(g+h)=(fg)+(fh)$	$f*(g+h)=(fg)+(fh)$

补充有关卷积的一些知识点

卷积之后图像大小

若卷积核和图像的大小分别为$m×n$和$M×N$，则在图像的顶部和底部分别补上$(m-1)$行0，在图像的左侧和右侧分别补上$(n-1)$列0，在这些条件下，卷积之后的图像大小为
$$ S_v=m+M-1 \quad S_h=n+N-1 $$

卷积可压缩

原理：卷积运算满足交换律

对于Q阶段的滤波器，如果一个图像$f$首先通过卷积核$w_1$，之后又通过卷积核$w_2$，以此类推，则滤波可在单阶段完成$w*f$，其中
$$ w=w_1 * w_2 * w_3 * \cdots * w_Q $$

数字图像处理基础（二）

概念